私たちは、2つの音の高さの違いの大きさ（音程）を、2つの音の音波の周波数比によって把握します。周波数比が同じであれば、音程が同じに聞こえます。
オクターブの周波数比が1:2であることはすでに述べました。では、それ以外の音程の周波数比はどれくらいでしょうか。

十二平均律

• ピアノなどでは、すべての半音の大きさが同じです。そういった調律法を「十二平均律」と呼びます。十二平均律では、半音はオクターブの12分の1です。すなわち、1:2の周波数比の12分の1です。同じ比率を12回繰り返すと2倍になるということですから、半音は2の12乗根（12分の1乗）倍となり、およそ1:1.06となります。全音はその2乗で1:1.12、全音半は1:1.19、などとなります。

倍音

• C音を基準にして、C音の2倍の周波数の音、3倍の周波数の音がどれくらいの高さに聞こえるのか、を16倍までまとめて書いてみます。
• 「↓」は音が音符よりも低いことを、「↑」は高いことを表しています。
• 「ある音の○倍の周波数の音」を、その音の「第○倍音」と呼びます。また、基準になる音、つまり第1倍音に相当する音の方を「基音」と呼びます。
  
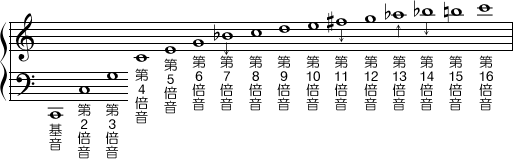
• 第2倍音は2倍の周波数の音ですから、オクターブ（完全8度）上の音になります。
• 第3倍音は3倍の周波数の音ですが、1オクターブと完全5度になります。十二平均律の完全12度（19半音）は1:2.997ですから、ほとんど一致します。
• 第4倍音は4倍ですから、2倍×2倍となりますので、1オクターブ（2倍）＋1オクターブ（2倍）、すなわち2オクターブになります。
• 第5倍音は、2オクターブと長3度になります。十二平均律の長17度（28半音）は1:5.04ですから、おおむね一致します。
• 第6倍音は6倍ですから、2倍×3倍となりますので、1オクターブ（2倍）＋1オクターブと完全5度（3倍）、すなわち2オクターブと完全5度になります。
• 第7倍音は、2オクターブと短7度よりかなり狭いが、2オクターブと長6度よりは、2オクターブと短7度に近い音程になります。
• 第8倍音は8倍ですから、2倍×2倍×2倍となりますので、3オクターブになります。
• 第9倍音は9倍ですから、3倍×3倍となりますので、1オクターブと完全5度＋1オクターブと完全5度、すなわち3オクターブと長2度になります。
• 第10倍音は10倍ですから、2倍×5倍となりますので、1オクターブ＋2オクターブと長3度、すなわち3オクターブと長3度になります。
• 第11倍音は、3オクターブと増4度よりかなり狭いが、3オクターブと完全4度よりは、3オクターブと増4度に近い音程になります。
• 第12倍音は、2倍×2倍×3倍となりますので、2オクターブ＋1オクターブと完全5度、すなわち3オクターブと完全5度になります。
• 第13倍音は、3オクターブと短6度よりかなり広いが、3オクターブと長6度よりは、3オクターブと短6度に近い音程になります。
• 第14倍音は、2倍×7倍となりますので、第7倍音の1オクターブ上の音になります。
• 第15倍音は、3倍×5倍となりますので、1オクターブと完全5度＋2オクターブと長3度で、3オクターブと長7度になります。
• 第16倍音は、2倍×2倍×2倍×2倍となりますので、4オクターブになります。
• 倍音は、楽器においては非常に重要な概念です。現代の金管楽器では、同じ倍音列の音を同じ指使いで演奏します。木管楽器でも、同じ指使いだったり似通った指使いだったりすることがあります。弦楽器でも「ハーモニクス」ないし「フラジオレット」と呼ばれる奏法は、倍音を使う奏法です。
• 一方で、通常の楽器の音には倍音の周波数の音が含まれています。独立した音として聞き分けることはできませんが、同時に鳴って、音色の違いとして感じます。オルガンでは、これらの倍音の音を意図的に組み合わせて、新しい音色を作り出します。

周波数比と音程

• 上の倍音列で、隣同士の音程を見てみましょう。
• 最初は周波数比が1:2ですが、完全8度です。
• 次は2:3で、完全5度です。
• 3:4は完全4度です。
• 4:5は長3度です。
• 5:6は短3度です。
• 8:9は長2度です。
• このように、単純な周波数比から、完全協和音程・不完全協和音程・不協和音程の順に並んでいます。このことから、古くから、音程の協和度は周波数比の単純さによると考えられてきています。
• このほか隣同士でないところで、さまざまな音程を見つけることができます。
• 第3倍音と第5倍音は長6度です。ですから3:5が長6度になります。（3:4の完全4度と、4:5の長3度の組み合わせ）
• 第5倍音と第8倍音は短6度です。ですから5:8が短6度になります。（長3度の転回音程）
• 第8倍音と第15倍音は長7度です。ですから8:15が長7度になります。（2:3=8:12の完全5度と、4:5=12:15の長3度の組み合わせ）
• 第9倍音と第16倍音は短7度です。ですから9:16が短7度になります。（長2度の転回音程）
• 第15倍音と第16倍音は短2度です。ですから15:16が短2度になります。（長7度の転回音程）