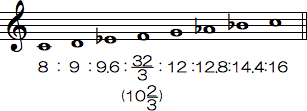音律とは、オクターブの中の音を、実際にどのような高さの音で演奏するか、ということです。もちろんここで大切なことは、絶対的な音の高さではなく、音の高さの違いの大きさです。

このページの約束

このページの記述を簡潔にするため、このページでは、オクターブ関係にある音は同じであると考えます。
これを音程で考えると、完全5度と完全12度（1オクターブと完全5度）、完全19度（2オクターブと完全5度）は同じ音程であるし、ある音の完全5度上の音と、完全4度下の音、は同じ音となります。
これを周波数で言うと、ある音の2倍、4倍、8倍、2分の1など、2の整数乗倍の周波数の音は、同じ音と考えます。
また周波数比で言えば、例えば1:3、2:3、4:3、また1:6、1:12の周波数比とは、すべて同じだと考えます。

音の響きと音程

• 倍音のページで、通常の楽器の音の中には倍音が含まれていると述べました。例えば100Hz（1秒間に100回の波があることを100Hzと言います）の楽器音には、第2倍音である200Hzや第3倍音である300Hzの周波数の音が含まれます。また、150Hzの楽器音にも、第2倍音に300Hzの周波数の音が含まれます。ですから、100Hzの楽器音と150Hzの楽器音には同じ300Hzの周波数の音が含まれていることになります。

  基音	第2倍音	第3倍音
  100Hz	200Hz	300Hz
  150Hz	300Hz	←一致↑

• ところが、一方の150Hzの楽器音をわずかに上げて151Hzにすると、その第2倍音は302Hzとなります。そうすると、100Hzの楽器音の第3倍音の300Hzの音と151Hzの楽器音の第2倍音の302Hzの音が同時に鳴ることになります。

  基音	第2倍音	第3倍音
  100Hz	200Hz	300Hz
  151Hz	302Hz	←ずれ↑

• このようなずれが生じると、音の揺れが感じられます。「ワンワンワン」のように聞こえます。これは音響学で「うなり」と呼ばれます。それを良しとするも悪いとするも好み次第、言い換えると音楽文化次第なのですが、ヨーロッパ音楽の中では一般に避けるべきとされる時代が長く続きました。このずれは、100Hz:150Hz、すなわち周波数比が2:3のような単純な整数比の場合には生ぜず、100Hz:151Hzのように単純な整数比でなくなると生じることになります。100:150も、100:151も、通常の私たちの耳には同じ音程に聞こえます。少なくとも、音楽的に同じ意味に受け取れます。ですから、100:150でも100:151でもいいはずなのですが、西洋音楽の中では、うなりを避けようと、同時に鳴る音をなるべく単純な整数比とするように、工夫されてきました。

セント

• ここで、私たちは、半音より狭い音の幅について考えていきます。そのようなとき、単位となるのが、「セント」と呼ばれるものです。「セント」は、十二平均律の半音の100分の1です。100セントで十二平均律の半音です。半音の周波数比は2の12乗根=1:1.059463ですが、1セントは2の1200乗根ですから、およそ1:1.000578の周波数比になります。例えば、さきほどの151Hzの音は150Hzの音の11.5セント上の音、と言うことができます。
• 一般に、音の高さの違いを耳で聞き分けられるのは、20セント程度から、と言われています。しかし、それより狭くても、2音が同時に鳴っているときには、うなりによって、音の高さの違うことを認識することはできます。

ピタゴラス音律

• 倍音のページで、1:3の音程は（1オクターブと）完全5度であると述べました。完全5度は完全に1:3でなくても完全5度に聞こえますが、完全5度の2つの音を同時に鳴らすとき、1:3であればうなりが生じません。このことから、1:3の周波数比を完全5度として積み重ねて、様々な音の高さを規定していくことが考えられました。一般にピタゴラスが発案したと言われることからピタゴラス音律と呼ばれます。また中国では三分損益法として古くから知られています。
• 次のように、完全5度上行（完全4度下行）を12回積み重ねると、異名同音に行き着きます。
  
  この例ではF音から始めて、12回目にEis音が出てきます。このEis音は、F音の3の12乗（3¹²）倍、つまり53万1441倍の周波数の音となりますが、F音であるならば2の17乗（2¹⁷）倍、つまり52万4288倍でならないのに対し、わずかに高くなります。どの音から始めても、異名同音に行き着いたときに、この周波数の違いが出てしまいます。これを違いを計算してみると、23.46セントであることがわかります。
• この23.46セントをピタゴラス・コンマと呼んでいます。コンマとは音律のもたらす微妙な音の高さの差のことです。
• この音律では、鍵盤楽器であれば、異名同音のためにそれぞれ別の鍵盤を用意するか、異名同音のどちらかの音に妥協するかを選ぶことになります。オクターブの中に12を超える鍵盤を用意することは実用的でないので、妥協する、すなわちどこかの完全5度に、さきのピタゴラス・コンマを含む完全5度を置くことになり、その完全5度が濁って聞こえることになります。ヴァイオリン属の楽器や声楽でも、異名同音のどちらかを選ぶことができればそちらで演奏すればいいですが、実際には楽譜の中に異名同音を同じ音として扱うことは出現するので、そこで何らかの妥協をすることになってしまいます。他の楽器でも大なり小なり演奏上の問題を抱えることになります。
• ピタゴラス音律は、limit 3の音律と呼ぶことがあります。第3倍音までを考慮した音律、ないし、因数に3までの数だけを含んだ数同士の周波数比から構成される音律、の意味です。
• ピタゴラス音律では、長3度をきれいに響かせることができません。それについては次の節で説明します。

純正律

• ピタゴラス音律は、長3度をきれいに響かせることができません。なぜならピタゴラス音律は長3度を完全5度を4つ積み重ねた音程として作りますが、
  
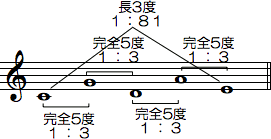
  それは3⁴倍、つまり1:81となり、単純な整数比とは呼べないからです。長3度としてよりふさわしいのは1:5です。ピタゴラス音律の長3度をこれと比べてみると、81:80（80は5×2⁴）の違いがあります。セントを計算すると21.51セントになります。これをシントニック・コンマと呼びます。
• これをなんとか解決しようとするのが純正律です。純正律では、長3度が出現したとき、この周波数比を1:5にします。
• たとえば、長音階は、3つの主要三和音から構成されます。I、IV、Vです。この主要三和音がそれぞれ1:5:3（4:5:6）となるようにします。
  
  
• こうして得られた音を音階に並べてみると、次のようになります。（次の譜例では、主音を8としてその周波数比を表しています）
  
  
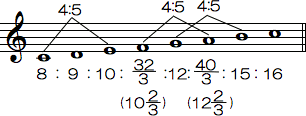
• この音階では全音（長2度）に、8:9の周波数比のところ（i−ii、vi−v、vi−vii）と、9:10の周波数比のところ（ii−iii、v−vi）とがあります。8:9を「大全音」、9:10を「小全音」と呼んで区別します。
• このようにすると、主要三和音はきれいに響かせることができます。しかし、たとえばII度の和音では、根音であるii度音と第5音であるvi度音の完全5度の周波数比が27:40となり、きれいに響きません。そのまま演奏するか、音高を自由に変化させることのできるヴァイオリン属の楽器や管楽器などでは、その都度正しくなるように音の高さを調整したりすることになります。
• 同じようにして自然短音階を考えてみましょう。自然短音階ではI、IV、Vの三和音をすべて短三和音で考えます。短三和音の第3音は短3度ですから、5:3の周波数比になります。第5音は長三和音と同じ1:3の周波数比ですが、第3音とそろえて5:15と考えましょう。すなわち短三和音の根音、第3音、第5音の5:3:15の周波数比になります。オクターブをそろえると10:12:15ですね。
  
  これを音階に並べてみます。主音を8に揃えるために、10:12:15を、IV度では（それぞれの項にをかけて）:12.8:16、I度では（それぞれの項に0.8をかけて）8:9.6:12、V度では（それぞれの項に1.2をかけて）12:14.4:18(9)と書いています。
  
  
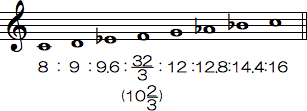
• 純正律は、limit 5の音律と呼ぶことがあります。第5倍音までを考慮した音律、ないし、因数に5までの数だけを含んだ数同士の周波数比から構成される音律、の意味です。

平均律

• 先ほど、長調の純正律では、ii度音とvi度音の完全5度がきれいに響かないと書きました。これは、シントニック・コンマのせいなのですが（本来なら1:3=27:81となるべき完全5度が、27:80（40）となる）この、シントニック・コンマの21.51セントを、4回の完全5度に等しく振り分けてしまおう、と考えた人がいました。完全5度は1:3の周波数比よりも5.38セント狭くなりますが、5.38セントならば（うなりは生じても）耳で判別することはできなくなります。4回の完全5度を振り分ければ当然2回の長2度（完全5度が2回）も振り分けられますので、大全音と小全音は均されます。これを中全音と言いますが、この方法による音律を中全音律と呼びます。また、このように、コンマを平均的に振り分けて音程の大小を均すような音律を、平均律と呼びます。
• 中全音律は、音律としては長3度が1:5で響くので純正律的ですが、考え方としてはピタゴラス音律に近いもので、完全5度を11回取ることで十二の半音の音を求めることができます。しかし、それでも、12回目の完全5度で異名同音に行き着くとき、最初の音と一致しなくなります。なぜなら12回目の完全5度とは4回の完全5度が3つであり、4回の完全5度とは長3度のことですから、すなわち3回の長3度なのです。3回の長3度とは1:5ですから、1:125、すなわち128:125ですから、この異名同音はピタゴラス音律とは逆にだいぶ低くなってしまいます。
• このようにして、音程の自由のきかない鍵盤楽器等の楽器のためにさらに様々な音律が考え出されますが、最終的に、ピタゴラス音律から、ピタゴラス・コンマを12の完全5度に均した音律が考え出されます。ピタゴラス音律よりもすこしだけ完全5度を狭く取りますので、ピタゴラス音律よりは多少は長3度が1:5に近づくのです。こうしてできたのが十二平均律です。12の完全5度を同じ広さにして異名同音を同じ高さにしたため、すべての半音が同じ幅となっています。

関連サイト

• 2つの音の周波数から、セントを算出する