これまで幹音同士の音程について考えてきましたが、ここでは派生音のはいった音の音程を考えます。
派生音と音程
- 音程を構成する音のうち、上の音に♯が付いて半音上がると、音程は半音広くなります。たとえば短2度は長2度になります。長2度(1全音)は短2度(1半音)より半音広いからです。
- 音程を構成する音のうち、下の音に♭が付いて半音下がっても、音程は半音広くなります。たとえば短3度は長3度になります。長3度(2全音)は短3度(1全音1半音)より半音広いからです。
- 音程を構成する音のうち、上の音に♭が付いて半音下がると、音程は半音狭くなります。たとえば長3度は短3度になります。
- 音程を構成する音のうち、下の音に♯が付いて半音上がっても、音程は半音狭くなります。たとえば長2度は短2度になります。
- 音程を構成する2音に、同じ臨時記号が付いたとき、2音は平行移動するのですから、音程は変わりません。

- このように、短音程は半音広くなると長音程になり、長音程は半音狭くなると短音程になります。
- また、減5度は半音広くなると完全5度になり、完全5度は半音狭くなると減5度になります。
- その転回音程の、増4度は半音狭くなると完全4度になり、完全4度は半音広くなると増4度になります。

- 変化記号が付いても、「度」を表す数字は変わりません。
- 変化記号には臨時記号の他に調号もあります。調号の場合も臨時記号と全く同じに考えます。
音程の分類
- これまでに出てきた、完全1、5度、長短2、3度、減5度およびその転回音程(完全4、8度、長短6、7度、増4度)を、「全音階的音程」と呼びます。
- 全音階的音程の内、完全1、5度、長短3度およびその転回音程(完全4、8度、長短6度)を、「協和音程」(協音程)と言います。
- 協和音程の内、完全1、5度およびその転回音程(完全4、8度)を「完全協和音程」(完全協音程)と呼びます。
- 協和音程の内、完全協和音程以外の音程、すなわち」長短3度およびその転回音程(長短6度)を、「不完全協和音程」(不完全協音程)と呼びます。
- 全音階的音程以外の音程を「半音階的音程」と呼び、次の節で見てゆきます。
- 半音階的音程を含め、協和音程以外の音程をすべて、「不協和音程」(不協音程)と呼びます。
| 全音階的音程
|
協和音程
|
完全協和音程
|
完全1、5度および転回音程
|
| 不完全協和音程
|
長短3度および転回音程
|
| 不協和音程
|
長短2度、減5度および転回音程
|
| 半音階的音程
|
不協和音程
|
その他の音程
|
半音階的音程
- 音程を構成する音に変化記号が付くと、全音階的音程では説明できない音程になることがあります。それらの音程を半音階的音程と言います。
- 完全5度より半音狭い音程は減5度でした。完全4度、完全8度を変化記号で半音狭くした音程も、減4度、減8度と呼びます。
日本語では、「オクターブ」とは「完全8度」のことです。
- 短音程を変化記号で半音狭くする音程も、減音程になります。たとえば、短3度を変化記号で半音狭くした音程は、減3度です。

- 完全4度より半音広い音程は増4度でした。完全1度、完全5度、完全8度を変化記号で半音広くした音程も、増1度、増5度、増8度と呼びます。
- 長音程を変化記号で半音広くする音程も、増音程になります。たとえば、長3度を変化記号で半音広くした音程は、増3度です。

- 増音程をさらに変化記号で半音広くした音程は、重増音程になります。

- 減音程をさらに変化記号で半音狭くした音程は、重減音程になります。

- 以上をまとめると、次の表になります。黒い線は半音の違いを表します。転回音程は、緑の縦線を対称軸に、線対称の所に行きます。

- 変化記号が付いても「度」を表す数字が変わらないのは、半音階的音程でも同じです。
- 度ごとに半音数をまとめると次のようになります。このまま覚える必要はありませんが、理解の手助けになるかも知れません。
| -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|
| 1度 | | 完全 | 増 | 重増 | | | | | | | | | | | | |
|---|
| 2度 | 重減 | 減 | 短 | 長 | 増 | 重増 | | | | | | | | | | |
|---|
| 3度 | | | 重減 | 減 | 短 | 長 | 増 | 重増 | | | | | | | | |
|---|
| 4度 | | | | | 重減 | 減 | 完全 | 増 | 重増 | | | | | | | |
|---|
| 5度 | | | | | | | 重減 | 減 | 完全 | 増 | 重増 | | | | | |
|---|
| 6度 | | | | | | | | 重減 | 減 | 短 | 長 | 増 | 重増 | | | |
|---|
| 7度 | | | | | | | | | | 重減 | 減 | 短 | 長 | 増 | 重増 | |
|---|
| 8度 | | | | | | | | | | | | 重減 | 減 | 完全 | 増 | 重増 |
|---|
特殊な半音階的音程
- 完全1度は全くの同音ですから、1度には完全1度より狭い音程はできません。つまり、減1度、重減1度はありません。
- 減2度(たとえばEとFes)は、ピアノの鍵盤では2音が同じ音になります。つまり、異名同音になります。
- 重減2度(たとえばEとFeses)は、ピアノの鍵盤では上下が入れ替わります。しかし、音の上下の関係は、楽譜の上での見かけ通りに考えます。
- 増8度と重増8度は、オクターブを超える音程(複音程)です。音程の転回のときなどの扱いが変わります。これについては後述します。
- 重増7度は、オクターブを超えていますが、扱いは複音程にはなりません。重減2度の転回音程です。
- 重減音程から重増音程までをもってしても、楽譜上のすべての音程が言い表されるわけではありません。たとえば、Ces-Disisは重増2度より半音広くなりますが、言い表し方はありません。
音程を調べる
- 2音間の音程を調べるには、次の手順を取ります。
- まず、変化記号(♯や♭)を取り除いてみます。
- その上で、2音の音程を調べます。
- まず、度数を調べます。ここで調べた度数は、最後まで有効です。
- 1、2、3、5度ならそのまま、それ以外なら転回して音程を調べその転回音程を得ます。
- 最初に付いていた変化記号が、何半音、音の幅を広げているか、または狭めているか、調べます。
- 上の表に従って、数字の前に付く名前を得ます。
- たとえば、

は、
- まず、

のように、変化記号を取り除いてみます。
- その上で、2音の音程を調べます、
- 度数は3度です。
- 3度で、覚えた中にありますから、長3度です。
- 下の音の♯と上の音の♭がそれぞれ1半音狭くしていますので、合計2半音狭くなっています。
- 長→短→減となりますので、減3度です。
- また、たとえば、

は、
- まず、

のように、変化記号を取り除いてみます。
- その上で、2音の音程を調べます、
- 度数は7度です。

のように転回してみます。2度になります。覚えた中にありませんから、長2度です。転回前の(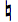 を付けた)2音の音程は、長2度の転回音程である短7度だったことになります。
を付けた)2音の音程は、長2度の転回音程である短7度だったことになります。
- 下の音の♭と上の音の♯がそれぞれ1半音広くしていますので、合計2半音広くなっています。
- 短→長→増となりますので、増7度です。
転回した状態で、変化記号を戻して音程を調べ、それを転回して答えを得る、という方法もあります。上の例なら、転回した2度のところで派生音を戻し、長2度より2半音狭い減2度を得ます。その転回音程から、増7度という答えを導き出します。
音程から音を調べる
- ある音の○○度上または○○度下の音を得るには、次の手順を取ります。
- まず、♯や♭は考えず、定められた音から定められた方向へ定められた度数だけ離れたところに、音符を書きます。
- 先の方法で、設問の音と、書いた音符の音程を調べます。
- 調べた音程が設問の音程と一致していれば、その書いた音符が答えです。
- 一致しない場合、上の表に従って、何半音広げなければならないか、または狭めなければならないか、調べます。
- 調べた結果に従って、書いた音符の前に臨時記号を書きます。
- 上の音を求める問題の場合、
- 1半音広げるには♯を、
- 2半音広げるには
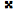 を、
を、
- 1半音狭めるには♭を、
- 2半音狭めるには
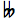 を、
を、
上の音に付けます。
- 下の音を求める問題の場合、
- 1半音広げるには♭を、
- 2半音広げるには
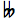 を、
を、
- 1半音狭めるには♯を、
- 2半音狭めるには
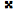 を、
を、
下の音に付けます。
- たとえば、

の長3度上の音を求めるには、
- まず、この音の3度上に音符を書きます。設問の♭と「長」は考えません。

- この2音の音程を調べます。♭を外してみます。

短3度です。しかし、下の音に♭が付いてたのですから、短3度より半音広い長3度です。
- 設問の「長3度」と一致しますから、これが答えです。

- またたとえば、

の減4度下の音を求めるには、
- まず、この音の4度下に音符を書きます。設問の♭と「減」は考えません。

- この2音の音程を調べます。♭を外し、4度なので転回してみます。

覚えた中にあるので、減5度です。ですから転回前の音程は増4度です。しかし、上の音に♭が付いたのですから、増4度より半音狭い完全4度です。
- 「完全4度」は設問の「減4度」と一致しませんから、次の段階に進みます。
- 設問の減4度は、表を見ると、完全4度よりも半音狭い音程です。
- 下の音を求める問題ですから、下の音に変化記号を付けて、半音狭めます。そのためには、下の音を半音上げなければなりません。つまり、♯を付けます。

設問の音に付いている変化記号を、最後の段階で戻す方法もあります。上の例なら、変化記号のない段階の増4度と減4度を比べ、「2半音狭くする必要がある」を得ます。ところが、設問となっている上の音にすでに♭がついて1半音狭くなっていますから、残りの1半音を答えとなる下の音に♯を付けて解決します。
一方、このような転回して考える音程においては、最初から転回音程で考えて、最後に転回し返すという方法もあります。つまり、「減4度下」を転回音程の「増5度上」と考え、Fis音を得ます。これを転回するためにオクターブ下げれば、答えの「減4度下の音」になります。またたとえば「増6度上」という問題ならば、増6度の転回音程の減3度を、設問の逆の方向、つまり設問の音の下に取ります。そうして得た音を、転回するためにオクターブ上げれば、問題に答えることができます。
問題
関連サイト














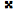 を、
を、
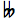 を、
を、
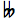 を、
を、
 を、
を、







